Непрерывные сигналы описываются непрерывными функциями времени. Мгновенные значения таких сигналов изменяются во времени плавно, без резких скачков (разрывов). Пример временной диаграммы непрерывного сигнала приведен на рисунке 1а. Сигналы, временные диаграммы которых изображены на рисунке 2, не являются непрерывными, поскольку их мгновенные значения в некоторые моменты времени изменяются скачками.
а)
б)
в)
г)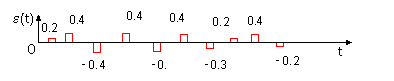 
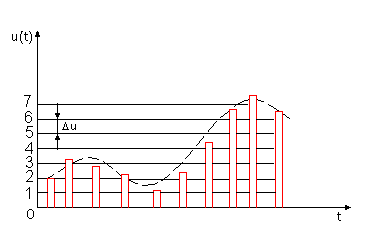
Рисунок 1 – Дискретизация, квантование непрерывного сигнала: а – непрерывный сигнал, б – дискретный по времени (импульсный) сигнал, в – дискретный по времени и значениям (цифровой) сигнал, г – ошибка квантования
Рисунок 2 – График реализации телефонного сигнала
Сигналы с дискретным временем можно получить из непрерывных сигналов, выполняя над непрерывными сигналами специальное преобразование, называемое дискретизацией по времени. Смысл этих преобразований проиллюстрирован с помощью временных диаграмм на рисунке 1.
Цифровые сигналы
При передаче импульсных сигналов в электросвязи часто применяют специальное преобразование, состоящее в следующем. При передаче каждый импульс может иметь амплитуду лишь с разрешенным значением. Число разрешенных значений амплитуд импульсов конечно и задано. Например, на рисунке 1в разрешенные значения амплитуд пронумерованы цифрами 1, 2, 3, …; величина ?u равна разности между любыми двумя соседними разрешенными значениями амплитуд. Если истинное значение амплитуды импульса сигнала u?(t), подлежащее передаче, попадает между разрешенными значениями, то амплитуду передаваемого импульса принимают равной разрешенному значению, являющемуся ближайшему к истинному. Такое преобразование называют квантованием, совокупность разрешенных значений амплитуд передаваемых импульсов называют шкалой квантования, а интервал ?u между соседними разрешенными значениями – шагом квантования.
Последовательность импульсов, полученная в результате квантования импульсов сигнала u?(t), также является импульсным сигналом, для которого введем значение uц(t). Особенность этого сигнала состоит в том, что амплитуда импульсов теперь имеет только разрешенные значения и могут быть представлены десятичными цифрами с конечным числом разрядов. Такие сигналы называют дискретными или цифровыми. Квантование приводит к ошибке квантования е(t) = uц(t) - u?(t). На рисунке 1г приведен пример временной диаграммы ошибки е(t). Передача цифрового сигнала uц(t) вместо сигнала u?(t) фактически эквивалентна передаче импульсного сигнала u?(t) с предварительно наложенным на него сигналом ошибки е(t).
Поскольку дискретные сигналы широко используют в настоящее время при передаче сообщений, а многие реальные сигналы (электрические сигналы при передаче речи, музыки, многих изображений) являются непрерывными, то важно знать: можно ли непрерывные сигналы представлять с помощью дискретных; можно ли указать условия, при которых такое представление оказывается точным. Ответы на эти вопросы дает доказанная в 1933 г. советским ученым Владимиром Александровичем Котельниковым и названная его именем теорема Котельникова. Эта теорема формируется следующим образом:
если непрерывный сигнал имеет спектр, ограниченный частотой Fмакс, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени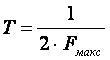 
, т.е. с частотой 
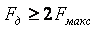, где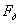 
- частота дискретизации; 
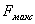- максимальная частота спектра сигнала.
Теорема Котельникова указывает условия, при которых непрерывный сигнал может быть точно восстановлен по соответствующему ему сигналу с дискретным временем.
Реальные непрерывные сигналы, подлежащие передаче, как правило, имеют спектры, хотя и довольно быстро стремящиеся к нулю с ростом частоты, но все же неограниченные. Такие сигналы могут быть восстановлены по своим дискретным отсчетам лишь приближенно. Но, если выбрать шаг дискретизации достаточно малым, то можно обеспечить пренебрежимо малое значение ошибки восстановления непрерывного сигнала по его переданным отсчетам в дискретные моменты времени.
К примеру, Fмакс для телефонного канала составляет 3,4 кГц. Следовательно, сигнал можно передать отдельными значениями, следующими с частотой 6,8 кГц, т.е. в одну секунду должно передаваться 6,8 тысяч отсчетов. Качество передачи речи при этом оказывается удовлетворительным. Увеличение частоты дискретизации сверх указанного значения допустимо и приводит к незначительному повышению точности восстановления телефонного сигнала.
Практическое занятие — 8
Тест
