Любое число можно выразить в следующей нормальной форме (такой способ еще называется экспоненциальной формой):
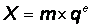
где
m- мантисса числа;
q - основание системы счисления; e - экспонента (порядок).
Для десятичной системы счисления число будет иметь вид:

Компьютерная версия такого представления называется
представлением с плавающей точкой.
Ниже приведены примеры чисел в такой записи:
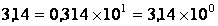
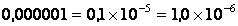
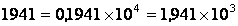
.
Как видно из примеров, существует несколько способов представления того или иного числа. Поэтому, для однозначности, в компьютерах используется нормальная нормализованная форма, в которой положение точки всегда задается перед значащей цифрой мантиссы, т.е. выполняется условие:
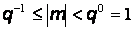 .
В общем случае вещественное число можно хранить в памяти компьютера в виде двоичного представления мантиссы и экспоненты.
.
В общем случае вещественное число можно хранить в памяти компьютера в виде двоичного представления мантиссы и экспоненты.
Последовательность разрядов содержит:
- разряд для знака мантиссы
- r цифровых разрядов для q-ичного модуля мантиссы
- разряд для знака порядка
- s разрядов для q-ичного модуля экспоненты
Диапазон представления модулей чисел в нормальной нормализованной форме определяется неравенством:

В конкретной ЭВМ диапазон представления чисел с плавающей точкой зависит от основания системы и числа разрядов для представления экспоненты.
Округление чисел. Рассмотрим представление
R с трехзначной мантиссой со знаком в диапазоне
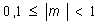
и двухразрядной экспонентой со знаком,
эти числа находятся в диапазоне от
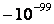
до

.
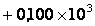
на 3 нельзя выразить точно в нашей системе представления.
Если полученное число нельзя выразить
в используемой системе представления, нужно брать ближайшее число, которое представимо в этой системе.
Такой процесс называется округлением.
Точность округления зависит от промежутков между смежными числами, которые (промежутки) не постоянны.
Промежуток между числами
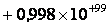
и
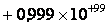
гораздо больше промежутка между числами и .
Однако, если промежутки между числом

и
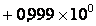
его соседом выразить как процентное отношение от этого числа,
большой разницы в промежутках не будет. Другими словами,
относительная погрешность, полученная при округлении,
приблизительно равна и для малых, и для больших чисел.
Выводы, сделанные для системы представления с трехразрядной мантиссой и двухразрядной экспонентой, справедливы и для других систем представления чисел. При изменении числа разрядов в мантиссе или экспоненте просто меняется число представляемых единиц в этих областях. С увеличением числа разрядов в мантиссе увеличивается плотность элементов и, следовательно, точность приближений. С увеличением количества разрядов в экспоненте расширяется область определения чисел за счет уменьшения точности.
Стандарт IEEE 754. В настоящее время большинство процессоров содержат команды с плавающей точкой, которые соответствуют стандарту IEEE 754 (IEEE, 1985). Стандарт определяет три формата: с одинарной точностью (32 бита), с удвоенной точностью (64 бита) и с повышенной точностью (80 битов).

Рисунок 1 - Форматы для стандарта IEEE с плавающей точкой: одинарная точность (а), удвоенная точность (б), повышенная точность (в)
Все форматы начинаются со знакового бита для всего числа: 0 указывает на положительное число, а 1 - на отрицательное. Затем следует смешанная экспонента, т.е. к ней прибавляется число так, чтобы экспонента всегда была неотрицательной. Для формата одинарной точности прибавляется 127, для формата удвоенной точности смещение - 1023, для повышенной точности - 16383. Всегда неотрицательная экспонента избавляет от необходимости выделять один бит для хранения ее знака и упрощает выполнение операций сравнения экспонент и арифметических операций над ними.
Нормализованная мантисса начинается с двоичной запятой, за которой следует 1 бит, а затем остаток мантиссы. Однако 1 бит перед мантиссой сохранять не нужно поскольку можно просто предполагать, что он есть. Следовательно, стандарт определяет мантиссу следующим образом: она состоит из неявного бита, который всегда равен 1, неявной двоичной запятой, за которыми идут 23, 52 и 64 произвольных бита. Если все биты мантиссы равны 0, то мантисса имеет значение 1,0. Если они равны 1, то числовое значение мантиссы немного меньше 2,0.
Существуют традиционные проблемы, связанные с числами в компьютере - это определения их переполнения, потери значимости и инициализации. Для этого в стандарте IEEE, помимо нормализованных чисел, предусмотрено еще 4 типа чисел (Рисунок 2).

Рисунок 2 - Числовые типы стандарта IEEE
Возникает проблема в том случае, если абсолютное значение (модуль) результата
меньше самого маленького нормализованного числа с плавающей точкой, которое можно
представить в этой системе. Раньше аппаратное обеспечение действовало одним из двух
способов: либо устанавливало результат на 0, либо вызывало ошибку из-за потери значимости.
Ни один из двух способов не является удовлетворительным, поэтому в стандарте IEEE введены ненормализованные числа.
Неявный бит 1 слева от двоичной запятой превращается в 0.
Ненормализованные числа можно легко отличить от
нормализованных, поскольку у последних не может быть экспоненты 0.
В этой схеме присутствуют два нуля, положительный и отрицательный, определяемые по знаковому биту. Оба имеют экспоненту 0 и мантиссу 0. Здесь тоже бит слева от двоичной запятой по умолчанию 0, а не 1.
С переполнением нельзя справится постепенно. Вместо этого существует специальное представление бесконечности: с экспонентой, содержащей все единицы, и мантиссой, равной 0. Это число можно использовать в различных математических выражениях - оно подчиняется обычным математических правилам для бесконечности.
Работа ЭВМ осуществляется под управлением программы, хранимой в памяти, как совокупность машинных команд.
Адрес очередной команды хранится в счетчике команд. По этому адресу из памяти выбирается команда и помещается в регистр команд. Команда состоит из кода операции и адресной части. Адресная часть указывает на место размещения операндов. Код операции дешифрируется дешифратором команд и соответствующий сигнал с выхода инициирует микропрограмму.
Микропрограмма - это последовательность микрокоманд, обеспечивающая выполнение данной операции.
Микрокоманда - совокупность микроопераций выполняемых в одном машинном такте. В частном случае может быть одна микрооперация.
Микрооперация - элементарное действие (например: обнуление регистра, прием кода и т.д.).
Основные структурные единицы памяти ЭВМ - это бит, байт, машинное слово.
Машинное слово - это структурная единица памяти, которая обрабатывается процессором за одно обращение.
Положительные числа всегда представляются с помощью прямого кода, но отрицательные числа в памяти ЭВМ представляются с помощью дополнительного кода.
А - В = А + (- В) - при выполнении операции вычитание компьютерное представление отрицательного числа должно быть в дополнительном коде - это позволяет операцию вычитание заменить операцией сложения.
Практическое занятие — 4
Тест



