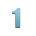
Определить прямой код двоичного числа: 10011011 (k=3, n=8).
Решение: k - знак числа, следовательно, 000 (положительное); n=10011011. Прямой код числа равен: 00010011011.
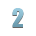
Определить обратный код двоичного числа: -10011011 (k=3, n=8).
Решение: чтобы определить обратный код числа, необходимо инвертировать все значения, кроме тех, которые относятся к группе "k". Таким образом, k - знак числа, следовательно, 111 (отрицательное); 10011011 > 01100100. Обратный код числа равен: 11101100100.
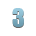
Определить дополнительный код двоичного числа: -10011011 (k=3, n=8).
Решение: чтобы определить дополнительный код числа, необходимо прибавить единицу к обратному коду числа. Таким образом, k - знак числа, следовательно, 111 (отрицательное); 10011011 > 01100100 (обратный код числа) > 01100101. Дополнительный код числа равен: 11101100101.

Определить двоичное число по его прямому коду: 11110011011 (k=3, n=8).
Решение: k - знак числа, следовательно. 11110011011 (111 = "-"), n - целая часть числа, следовательно, 10011011 - целая часть. Двоичное число: -10011011.

Определить двоичное число по его обратному коду: 11110011011 (k=3, n=8).
Решение: k - знак числа, следовательно. 11110011011 (111 = "-"), n - целая часть числа, следовательно, 10011011 - целая часть. Таким образом, 10011011 > 01100100 (прямой код числа). Двоичное число: -01100100.
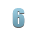
Определить двоичное число по его дополнительному коду: 11110011011.
Решение: k - знак числа, следовательно. 11110011011 (111 = "-"), n - целая часть числа, следовательно, 10011011 - целая часть. Таким образом, 10011011 (дополнительный код) > 10011010 (обратный код) > 01100101 (прямой код). Двоичное число: -01100101.
Практическое занятие — 7
Теория



