В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере (например, выпал номер 15)?
Решение: Поскольку вытаскивание любого из 32 шаров равновероятно,
то количество информации об одном выпавшем номере находится из уравнения:
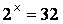
, но
.
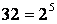
Очевидно, ответ не зависит от того, какой именно номер выпал.
Сколько информации несет сообщение: "В субботу я иду в гости"?
Решение: В гости можно пойти в любую субботу года. Число суббот в году: 12 х 4 = 48.
Таким образом, информация находится из уравнения:
.
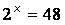
Решение этого уравнения:
.
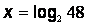
Из
таблицы логарифмов следует (с точностью до 3-х знаков): х = 5,585.
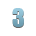
При бросании монеты сообщение о результате жребия (например, выпал орел) несет 1 бит информации, поскольку количество возможных вариантов результата равно 2 (орел или решка). Оба эти варианта равновероятны.
Решение: Ответ может быть получен из решения уравнения:
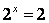
, откуда следует: x=1 бит.
При игре в кости используется кубик с шестью гранями.
Сколько бит информации получает игрок при каждом бросании кубика?
Решение: Выпадение каждой грани кубика равновероятно.
Поэтому количество информации от одного результата бросания находится из уравнения:
.
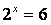
В данной задаче число N не равно целой степени двойки, следовательно, решение этого уравнения:
.
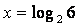
Из
таблицы логарифмов следует (с точностью до трех знаков после запятой):
.
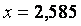
Книга, набранная с помощью компьютера, содержит 150 страниц; на каждой странице 40 строк, в каждой строке 60 символов. Каков объем информации в книге?
Решение: Мощность компьютерного алфавита равна 256. Один символ несет 1 байт информации. Значит страница содержит 40 х 60 = 2400 байт информации. Объем всей информации в книге (в разных единицах):
2400 х 150 = 360 000 байт > 360 000/1024 = 351,5625 Кбайт > 351,5625/1024 = 0,34332275 Мбайт.
В коробке имеется 50 шаров. Из них 40 белых и 10 черных. Определить количество информации в сообщении о попадании белого шара и черного шара.
Решение: Сначала необходимо определить вероятности попадания при вытаскивании шаров. Обозначим pч - вероятность попадания при вытаскивании черного шара, рб - вероятность попадания белого шара. Тогда: рч=10/50=0,2; рб=40/50=0,8.
Теперь можно определить количество информации: iч=log2(1/0,2)=log25=2,321928; iб=log2(1/0,8)=log2(1,25)=0,321928.
Практическое занятие — 2
Теория
